STL priority_queue优先队列

优先队列是一种容器适配器，队列元素要求实现了严格弱排序（Strict Weak Ordering），保证队列顶点（top）元素始终为最大值（最小值）。

优先队列本质上是一种堆，默认最大堆，即每一个父节点的值都比其子节点要大，因此根节点中的元素总是树中的最大值，因此常用于最值的读取。在时间复杂度上，优先队列实现单个元素的增删都是O(log n)，而读取队列顶点则为O(1)

接口原型 🔎

如下接口定义可以看出，优先队列的定义包含三个元素：

• 元素类型T；
• 存储元素的基础容器类型，要求为拥有连续内存分布的SequenceContainer， STL中满足的就是std::vector and std::deque两种了；
• 元素比较函数Compare， Compare函数主要用于元素比较，实现严格的弱排序，由于排序，优先队列已经不满足“先进先出”的特性了。

template <class T, class Container = vector<T>,
  class Compare = less<typename Container::value_type> > class priority_queue;

主要成员函数

所有STL标准库实现的数据结构，都有对应的CRUD（增删改查）接口，形式也基本类似.

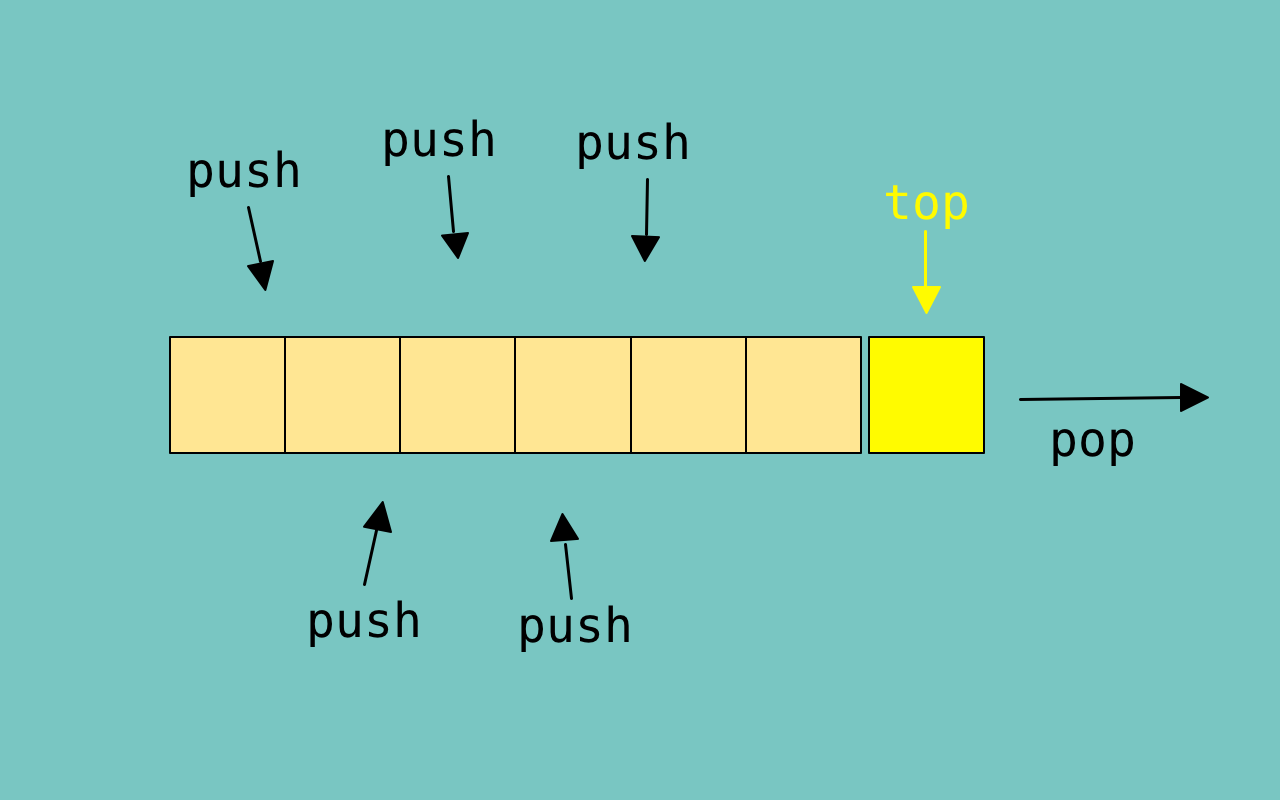
Comp函数

comp函数默认为使用仿函数std::less<int>,表示最大堆 ，这里less是降序，但由于优先队列将top指向了队列尾；同理，std::greater<T>,表示最小堆.

class Compare = less<typename Container::value_type> 

comp函数要求严格弱排序，那么什么是严格弱排序

维基百科给出了如下定义，简言之就是内置类型会通过!(a < b) && !( b < a ) 来判断ab是否相等，如果判断中携带了=如>=、<=，将导致相等判断逻辑出现错误。

A Strict Weak Ordering is a Binary Predicate that compares two objects, returning true if the first precedes the second. This predicate must satisfy the standard mathematical definition of a strict weak ordering. The precise requirements are stated below, but what they roughly mean is that a Strict Weak Ordering has to behave the way that “less than” behaves: if a is less than b then b is not less than a, if a is less than b and b is less than c then a is less than c, and so on.

另外当元素类型T为自定义类型时，那就需要自定义的comp函数，一般有实现后缀运算()函数 和 重载关系运算符 <、 > 两种方式

#include<queue> // priority_queue头文件
#include<functional> // 仿函数头文件

struct Node {
		int x, y; 
		node(int x, int y) : x(x), y(y) {} 
};
 
// <操作符用于仿函数std::less
// node比较先按照x降序，x相等时，再按照y降序
bool operator < (Node a, Node b) 
{ 
      if (a.x > b.x) {
					return true;
			} else if (a.x == b.x) {
					return a.y > b.y; // 严格弱排序
			} else {
					return false;
			}      
}

std::priority_queue<Node, std::vector<Node>, std::less<Node>> pq; // 大顶堆

// >操作符用于仿函数std::greater
bool operator > (Node a, Node b)
{
    return a.x> b.x;
}

std::priority_queue<Node, std::vector<Node>, std::greater<Node>> pq; // 小顶堆

// 自定义后缀操作符
struct cmp
{
    bool operator()(Node a,Node b)
    {
		  return a.x > b.x;
    }
};

std::priority_queue<Node, std::vector<Node>, cmp> pq;

例子

优先队列作为数据结构中堆的一种具体实现，在leetcode算法题中出现频率较高。比如这题leetcode 1792. Maximum Average Pass Ratio

在如下解答中，可以发现priority_queue的几个关键接口的使用。

另外算法层面可以看到，通过对优先队列进行增删读元素，使得每次都对最值进行操作，也就保证了每次操作都为最优解。实际上这就是贪心算法，通过求解每个子问题的最优解，来得到整个问题的最终最优解。也正因如此，优先队列就常在一些有约束条件下的分配问题。

class Solution {
public:
    // !!整数除法一定先转double, 注意检查括号
    // !!乘法注意溢出，少量的除法误差可以容忍
    #define cal(xy) ((double)(xy[0] +1) / (xy[1] + 1) - (double)(xy[0]) / (xy[1]))

    double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {
        priority_queue<pair<double, int>> qu; // 默认最大堆
        
        // 入队列，按照分配1个之后的差值，排序
        for (int i = 0; i < classes.size(); i++) {            
            qu.emplace(cal(classes[i]), i); // !!优先使用emplace/emplace_back， 比push/push_back更高效
        }
        
        while (extraStudents--) {
            auto [diff, i] = qu.top();
            qu.pop();
            
            
            // 从队列中取出差值最大的一项，即分配给它后结果最大的
            classes[i][0]++;
            classes[i][1]++;
            
            // 分配后重新塞回队列
            qu.push({cal(classes[i]), i});
        }
        
        auto maxsum = 0.0;
        for (auto c : classes) {           
            //cout << cal(c) << "-" << c[0] << "-" << c[1] << endl;
            maxsum += (double)c[0] / c[1];
        }
        
        return maxsum / classes.size();
    }    
};

⚠ Note: 转载请注明出处